Cumulative sum as a test for your programming environment
This post may be useful for those researchers and programmers, who work much with numerical crunching.
Have you ever tried to think about what will be coding like 10 years later? What processors and technologies will be used?
Typically we don’t care about such questions when writing our projects (unless those are a critical part of some important system). Or we theorize in this direction, but this never affects our code.
In principle, this is quite explainable: code written in C++ about 20-30 years ago is still working fine, without many changes in its structure. The speed increased thanks to technological process used in processors.
Processors and compilers changed much to increase execution speed, complex pipelines and automatic vectorization are used to make old-style programs running fast.
But there is some obvious limit your programming environment will not be able to overcome unless you explicitly took care about this. I’ll demonstrate it using a very trivial example — a cumulative sum.
The reference (abstract) code looks like:
input = given array x of length n
result = array of length n + 1
result[0] = 0
for i in 0, 1, .., n - 1:
result[i + 1] = result[i] + input[i]
Here I uses the zero-based indexing.
This is fairly trivial piece of code that C/C++/Fortran programmers write in their language without any hesitation. However, looking from perspective of 10-years-later coding, this trivial code may become the worst place in the program.
To understand this, let’s first look at changes in computing we can observe at this point. There were many talks over the years that possibilities of single core are exhausted (due to limitations of Si-based circuits), and we have to use many cores, or SIMDed processing units. Anyway, computers need to rely on parallel computations more and more.
But the code we wrote for cumulative sum is not parallelizable at all, the computations in cycle are chained,
next iteration shall be done exactly after previous. Unless you use some dangerous flag like -fmath, the
compiler will never be able (even in theory) to speed up this code, because otherwise it will have to break a summation order.
Summation order matters, because addition is not associative in floating-point numbers.
Ways to parallelize cumulative sum computation
There are different possible ways to make execution parallel, but this is not for free: the number of arithmetic operations will be at least doubled. Assuming, that we have $n$ samples and $m$ processing units, and also that $n = m \times \text{chunk}$ (we can extend initial arrays with zeros).
So each processing unit will work with subarray of length $\text{chunk}$.
n = m * chunk
input = given array x of length n
result = array of length n
subarray_sums = array of length m
for i in 0, 1, .., m - 1 in parrallel:
subarray_sums[i] = sum(result[i * chunk : (i + 1) * chunk])
# Now we can compute
result[0] = 0
for i in 0, 1, .., m - 1:
result[(i + 1) * chunk] = result[i * chunk] + subarray_sums[i]
for i in 0, 1, .., m - 1 in parallel:
for position in i * chunk, i * chunk + chunk - 1:
result[position + 1] = result[position] + input[position]
Numerical stability
Important question we have to keep in mind is that changing the order of computation may in theory drive to numerical instability (that’s why even smart optimizers don’t touch the computational graph), but in our case we reduced many unstable operations (add small number to large).
Now the computational flow consists of summing over chunk, sequential summation of $m$ numbers of comparable order, and again summation within chunk. This scheme is surely no worse that was initially (rare case, actually).
Current optimal implementation
Maybe after several years our co-processors will consist of hundreds of cores and present on every PC - who knows? At this moment usually we have 2-4 cores in laptops, so there is no drastic difference, and probably not much sense in using more complex code unless you’re going to use the code
The optimal implementation is available in numpy or MATLAB:
result = cumsum(input)
Eh… Trivial, right? This code is one-threaded (at this moment).
Why actually it is good idea to use third-party functions is that their implementation may be changed according
to the environment and situation. This is what already happened to many MATLAB operations.
People that were writing code in MATLAB 15 years ago had no idea, what is GPU. However,
today many of their programs are enjoying GPU acceleration. I.e. the GEMM operation is almost surely to be run on GPU today.
Contrary to this, fortran doesn’t provide any convenient way to perform computation of cumsum.
It would be funny to know years later that all the operation in your old code are parallelized, but trivial loop for cumulative sum is still running in one thread making the whole program slow.
 Gradient boosting
Gradient boosting 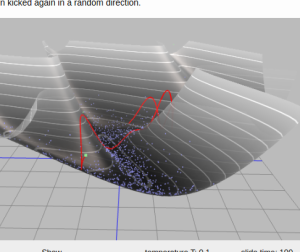 Hamiltonian MC
Hamiltonian MC 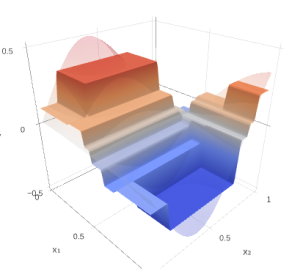 Gradient boosting
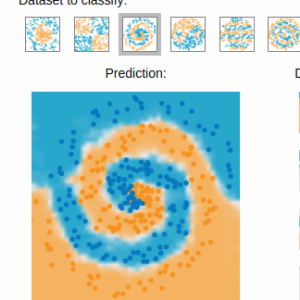
Gradient boosting  Reconstructing pictures
Reconstructing pictures 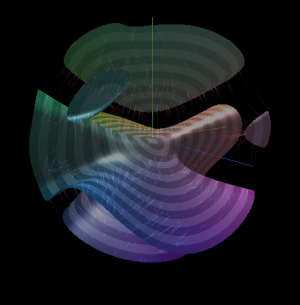 Neural Networks
Neural Networks